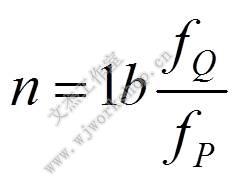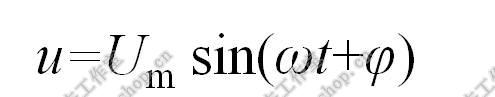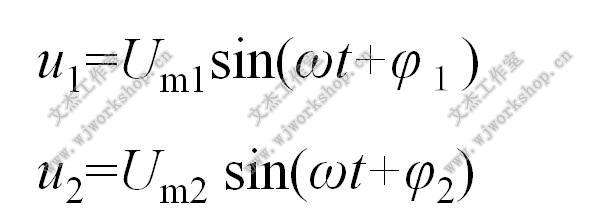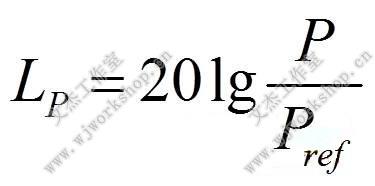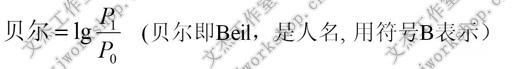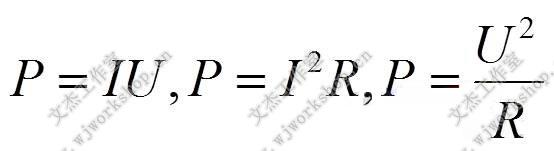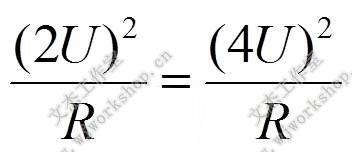1.1 频率、频谱、倍频程及相位
频率是电学和声学中的一个基本量。很多声学量都与频率有关,传声器灵敏度的校正、电声换能器频率特性的测量、厅堂音质的鉴定以及信号的分析都离不开频率。 频率是单位时间内信号振动的次数,一般用f表示,单位是赫兹(Hz)。
1 Hz(赫兹)=10-3 kHz(千赫兹)=10-6 MHz(兆赫兹)
在声学和电学领域里,频率一般是指正弦波信号的频率。 任何信号都可以认为是各种频率的正弦波叠加,或者说任何信号都含有正弦波的各种频率成分。 人们通过对各种频率成分含量的分析, 可以了解该信号的许多特性。例如,人的声音信号可以分解为各种频率正弦信号的叠加,通过频谱分析我们可以知道,男声的高频成分要比女声的高频成分少且幅度小,男声的低频成分要比女声的低频成分多且幅度大,故男声声音较低沉浑厚,女声声音较尖细。由此可见,对信号频率的分析是非常重要的。
人耳可听到的频率范围是20 Hz~20 kHz。 当然这只是一个大概的范围, 每个人实际上听到的频率范围并不相同,一般来讲,青年人要比老年人听到的频率范围要宽, 因为随着年龄的增长,人耳对高频声的听力会逐渐降低。
频率低于20 Hz的声波称为次声波; 频率高于20 kHz的声波称为超声波。 对于次声波和超声波,人耳是听不见的。
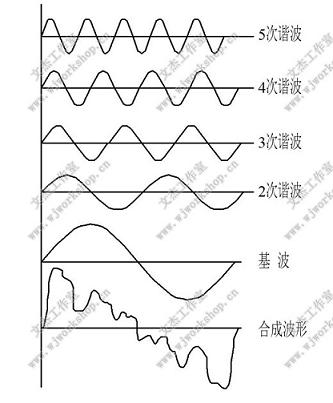
声音可以是单一频率的声音,称为纯音;而包含有几种不同成分的声音,则称为复合音。大多数的声音是由多个频率成分组合而成的复合音, 如语言、音乐或噪声大多是复合音。复合音都可以分解为许多纯音之和。如果复合音的大多数纯音都集中在高频部分,就称为高频声; 集中在低频部分,就称为低频声。当然,所谓高频声和低频声都是相对而言的,我们习惯上把频率低于60 Hz的声音称为超低音,把60~200 Hz的声音称为低音,把200 Hz~1 kHz的声音称为中音,把1~5 kHz的声音称为中高音,而把5 kHz以上的声音统称为高音。在复合音分解的信号中,频率最低的一个纯音成分称为基音;比基音频率高整数倍的纯音成分称为泛音。按频率从低到高依次称为第一泛音(谐波)、第二泛音和第三泛音等等, 如图 1-1所示。
2. 频谱
频率是对声音进行描述的一个基本参量, 它在时间上是连续的;而频谱分析则是对声音进行更为详细描述的一个重要手段。声音的频谱在时间上是离散的; 声音(复合音)的频谱结构是用基频、谐频(泛音)数目、各谐频幅度大小及相位关系来描述的。每个人的声音都有自己非常特别的惟一的频谱结构, 即每个人的声音都有自己的特色,正是因为这一特色的存在, 我们才常常能从电话的声音里立即听出是谁在同自己讲话。
3. 倍频程
倍频程是声学中常用到的一个概念, 可由下式表示:
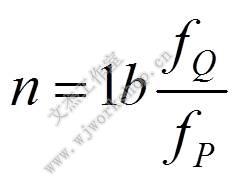
式中,fP为基准频率;fQ为求倍频程数的信号频率;n为倍频程数,可正可负,也可以是分数或整数。
频段的划分一般以倍频程为刻度单位。在音乐中,将一倍频程分为八度,即频率每提高一倍,音调提升八度。
4. 相位
相位是电学和声学的另一个基本量。在音响系统中,音质的改变与声音信号的相位有很大的关系,许多环绕声处理器(尤其是双声道环绕声处理器)就是通过一系列的处理过程, 对声音的相位进行了相应的改变最后进行合成而形成的。 另外, 音响系统中设备的调整、 连接等也和相位有诸多的关联。
例如, 若有一声音(单频)信号为
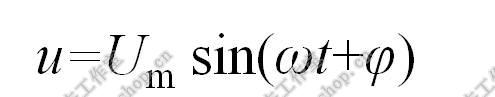
则称ωt+φ为相位角,称φ为初相角。若有两个同频声音信号:
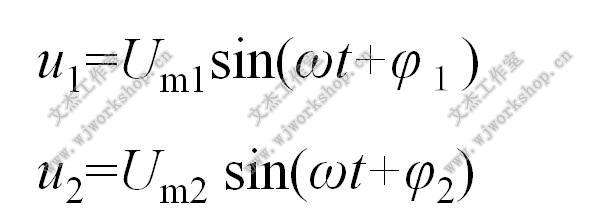
则称Δφ=(ωt+φ1)-(ωt+φ2)= φ1-φ2为u1 相对于u2 的相位差。其中:
若Δφ >0, 则u1超前u2一个Δφ ;
若Δφ <0, 则u1滞后u2一个Δφ ;
若Δφ =0, 则u1与 u2同相;
若Δφ =π/2,则u1与u2正交;
若Δφ =π, 则u1与u2反相。
1.2 声压及声压级
1. 声压
大气静止时存在一个压力,称为大气压。当有声音在空气中传播时,局部空间产生压缩或膨胀,在压缩的地方压力增加, 在膨胀的地方压力减小,于是就在原来的静止气压上附加了一个压力的起伏变化。这个由声波引起的交变压强称为声压, 一般用p表示,单位是Pa(帕)。
声压的大小反映了声音振动的强弱, 同时也决定了声音的大小。在一定时间内,瞬时声压对时间取均方根值后称为有效声压。 用电子仪器测量得到的通常是有效声压,人们习惯上讲的声压实际上也是有效声压。
声压是一个重要的声学基本量, 在实际工作中我们经常会用到,例如,混响时间是通过测量声压随时间的衰减来求得的; 扬声器频响是扬声器辐射声压随频率的变化;声速则常常是利用声压随距离的变化(驻波表)间接求得的。
2. 声压级
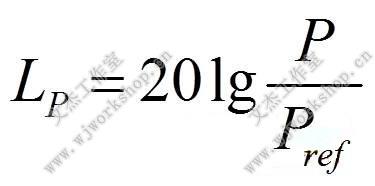
人耳有一个很奇怪的特点,其主观感受的响度并不正比于声压的绝对值,而是大致正比于声压的对数值。同时,人耳能听到的最低声压(听阈值)到人耳感觉到疼痛(痛阈值)的声压之间相差近一百万倍,因此用声压的绝对值来表示声音的强弱显然也是很不方便的。基于以上两方面的原因,我们常用声压的相对大小(称声压级)来表示声压的强弱。声压级用符号LP表示,单位是分贝(dB),可用下式计算:
式中,P为声压有效值,Pref为参考声压,一般取2×10-5 Pa,这个数值是人耳所能听到的1 kHz 声音的最低声压,低于这一声压, 人耳就再也无法觉察出声波的存在了。
1.3 反射、绕射及干涉
1. 反射
声波从一种媒质进入另一媒质的分界面时,会产生反射现象。 例如,声波在空气中传播时,若遇到坚硬的墙壁,一部分声波将反射。如图1-2(a)所示,反射角等于入射角时,反射声波好像从墙后的另一声源S′发出来一样,S′称为声像。声像S′与声源S到墙壁的距离相等。
当声波遇到凹面墙时,反射现象如图1-2(b)所示。声源S发出的声波经凹面墙后集中到一点S′,称为声波的聚焦。当声波遇到凸面时, 将产生扩散反射现象,如图1-2(c)所示。
当声波遇到障碍物时,除了产生反射现象外, 还有一部分声波将进入障碍物, 称为折射。障碍物吸收声波的能力与其特性有关。
声波的反射与折射现象是听音环境设计中需要考虑的问题。 演播室、 听音室、歌剧院和电影院中凹凸不平的墙面,就是为了使声波产生杂乱反射以形成均匀声场,并让墙壁吸收一部分能量, 使这些空间具有适当的混响时间。
2. 绕射
当声波遇到障碍物时,会有一部分声波绕过障碍物继续向前传播, 这种现象称为绕射。绕射现象示意如图1-3所示。绕射的程度取决于声波的波长与障碍物大小之间的关系。若声波的波长远大于障碍物长度尺寸,则绕射现象非常显著;若声波波长远小于障碍物长度尺寸,则绕射现象较弱,甚至不发生绕射。因此,对于同一个障碍物,频率较低的声波较易绕射, 而频率较高的声波不易绕射。
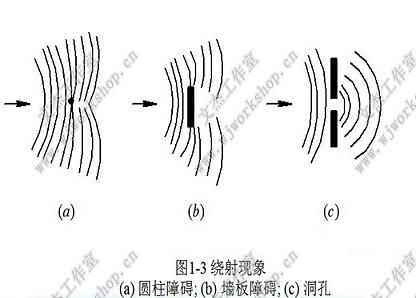
当声波通过障碍物的洞孔时,也会发生绕射现象。当声波波长远大于洞孔尺寸时,洞孔好像一个新的点声源,声波从洞孔向各个方向传播。 当声波波长小于洞孔尺寸时,只能从洞孔向前方传播。
由于绕射和反射的共同作用,从没有关严的门缝里传播到房间中的声波几乎和门打开时的不相上下。
这就告诉我们,连接音箱和功放时一定要保持它们正负极性的一致性,否则就会出现上述的第二种情况。当然,对于立体声系统而言,这样的结果往往还会导致声像定位不准,即声源有“飘忽”的感觉。
3. 干涉
两个频率相同、振动方向相同且步调一致的声源发出的声波相互叠加时就会出现干涉现象。如果它们的相位相同,两声波叠加后其声强加强,反之, 如果它们的相位相反,两声波叠加后便会相互减弱,甚至完全抵消, 如图1-4所示。 由于声波的干涉作用,常使空间的声场出现固定的分布,形成波腹和波节,即出现通常所说的驻波。驻波是干涉的一种特殊情况。顾名思义, 驻波有声波向前传播的运动, 也有不向前传播的运动。当两个频率相同、振幅相等、方向相反的正弦波同时存在时,由于它们的叠加,就变成了不传播的驻波。此时,空气的某些质点由于两个声波的振幅相反, 叠加后为零而不运动,称为波节; 而另一些质点在其中心位置振动, 振幅最大(等于两个声波的振幅之和),称为波腹。在波节和波腹之间的各点,质点运动规律处于波节与波腹的运动规律之间。
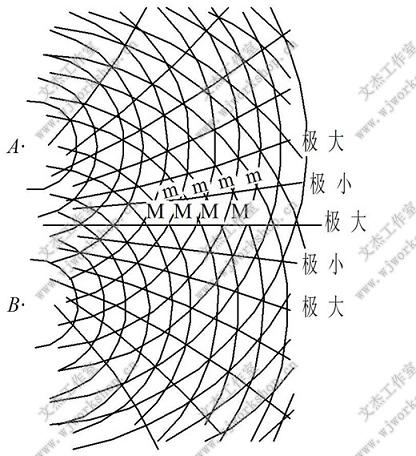
图1-4 干涉现象示意图
造成声波干涉的条件是经常可以遇到的,下面以两只扬声器播放同频率声音的情况为例来说明:
(1) 当两只扬声器在同相位状态下振动发声时,由于等距关系,声波到达两扬声器之间中轴线上的各点时总是处在同相位状态,于是来自两只扬声器的声波在该处相互加强。
(2) 当两只扬声器在反相位状态下振动发声时,情况正好相反,声波到达两扬声器之间中轴线上的各点时总是处在反相位状态,于是来自两只扬声器的声波在该处相互抵消,导致两只扬声器不如一只扬声器的声音大。
这就告诉我们,连接音箱和功放时一定要保持它们正负极性的一致性,否则就会出现上述的第二种情况。当然,对于立体声系统而言,这样的结果往往还会导致声像定位不准,即声源有“飘忽”的感觉。
1.4 分 贝 的 概 念
在电声技术中,表达放大器的增量、音响大小、噪声程度、 传输线的衰减等时,要用到dB(分贝)这一计量单位,尤其是在功率与功率之间或电压(流)与电压(流)之间作比较时,是用dB(分贝)表示来进行比较的。当我们用分贝表示功率、电压、 电流的大小时, 就是声功率级LW、声电压级LP和声强级LI以及级差ΔL。将庞大的电压值、功率值和电流值用分贝来表示,可以在比较小的数量范围里很方便地进行计算。
1. 功率和分贝的关系
分贝是一个相对值,而不是一个绝对值,这在前面讲解声压级的概念时就已经涉及到。分贝值是先选择一个参考值,然后再把需要表示的绝对值与这个参考值进行比较而得出的相对量。比如,选择参考功率值P0=1 W,P1是需要表示的功率值,那么
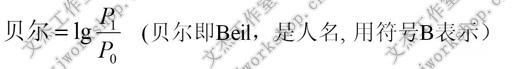
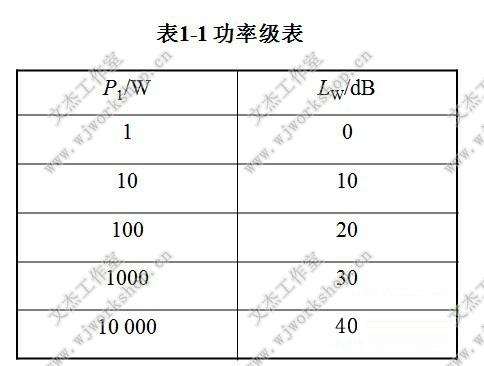
从表1-1 中可以看出功率从1~10 000 W,这样庞大的范围如果使用dB来表示, 即用单位的级来表示是很方便的。
另外,从心理学的角度来讲,功率增加10倍,多数人判断的结果是响度(是人耳对声音强弱的主观感受)增加1倍。这样的话,一个100 W的声音信号就是一个10 W声音信号响度的两倍。 任何10 dB的差值都可以不必考虑其实际功率的情况,均表示主观响度上相差一倍。 例如表1-1中相邻两信号的响度就相差一倍。
2. 电压、电流与分贝的关系
表示电压的dB也是一个相对值,需要一个基准电压U0和一个需要表示的电压U1。首先,我们来看看电功率和电压的关系:
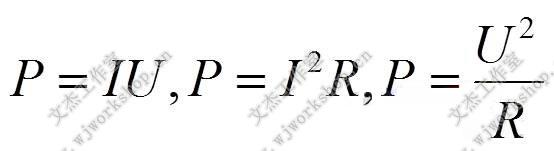
因为电功率和电压的平方成正比例,所以如果电压增加2倍, 功率就要增加4倍,即
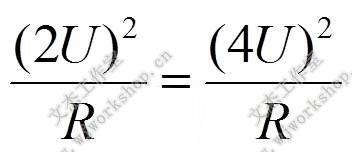
对电流也一样,即如果电流增加2倍,功率就要增加4倍。
用电压和电流比表示以dB为单位的功率级,则应为:

3. 调音台实际电压的分贝表达
我国规定,以一个600Ω电阻上得到1 mW功率所需的电压值0.755 V为基准电压U0,待比较电压Ux的电平值用分贝表示, 则

关于基准电压的选择,世界上许多国家对U0的电压选择有所不同。我国使用的U0为0.755 V,称为dBm,有些国家选用的U0为1 V,称为dBv。这样,实际使用时,基于不同基准电压选择的同一dB值,其所对应的实际电压是有差别的; 而同一实际电平所表示的dB值也不相同。表1-2 为dBm和dBv所代表的实际输出电压值。
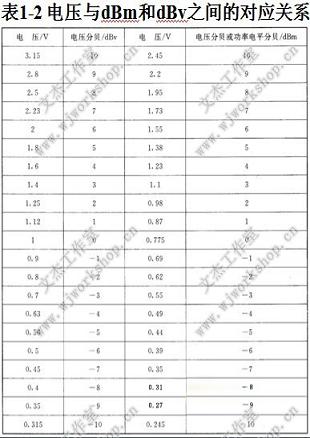
特别应引起调音员注意的是,现在有些调音台的VU表指示为0 dB时,其实际的输出电压为1.23 V。因此在使用调音台时, 一定要留意说明书上的介绍,因为这个具体的输出值是由生产厂家自己确定的。
4. 信噪比
如果用S表示信号,用N表示噪声,则信噪比为

式中:PS为信号功率,PN为噪声功率,US为信号电压,UN为噪声电压。
在音响技术中,频率响应、选择性、立体声分离度等均用到了分贝这一单位。